Binary Neural Network その2:「Binarized Neural Networks」を読みました
この記事は6/15に開催されたMETRICAエンジニア勉強会の発表資料です。
今回は参加者の西本くんがBinary Neurarl Networkについて発表してくれました。
Binarized Neural Networksの関連のある論文としてBinary Connectも解説してくれています。
背景
- Deep Learningの学習はエネルギー消費の多いGPUを使うことがほとんど。
- 近年low-powerなデバイス上でDeepLearningの計算を行うための研究も盛んに行われている。
Binarized Neural Networks (BNNs)
著者は重みだけでなく活性も2値化したBinarized Neural Networkを提案した。
これは、学習時は2値化された重みと活性を使って勾配計算し、2値化された重みと活性を用いて推論するようなNeural Networkのことである。
重みの2値化
決定的(Deterministic)な方法と、確率的(Stochastic)な方法がある。
- Deterministicな方法:

- Stochasticな方法


$\sigma(x)$はハードシグモイド関数である。 Stochasticな2値化は乱数発生器を必要とするので実装がやや困難である。 この論文においては、活性化に対してはいくつかの実験で学習時にStochastiな2値化を行うが、それ以外は専らDeterministicな2値化を行う。

学習時

勾配の計算と蓄積
- 誤差関数の勾配を計算する際は2値化された重みと活性を用いるが、勾配が蓄積され更新される重みは、高精度の実数値のままにしておく。SGDによりうまく重みの更新が行われるためには、更新される重みは高精度実数である必要があるからである。
- 重みと活性の2値化をノイズ付加とみなすことができる。DropOut, DropConnectの研究からわかるように、勾配計算の際に重みや活性にノイズを加えることは汎化性能向上に繋がり、正則化として機能する。特にBNNsは、勾配計算の際に、ランダムに活性の半分を0にするのではなく、活性と重みの両方を2値化するという点で、DropOutの変種と見ることができる。
実数の重み$W$の更新の際、$Update()$ (ADAM or Shift Based AdaMax) の結果を$ Clip() $ 関数で$-1 \sim 1$に押し込めている。
Batch Normalizationについて
Batch Normalizationは学習を早め、重みのスケールの影響を減らすが、都度標準偏差を計算して割る必要があり、掛け算の操作がたくさん必要になる。
代わりに、shift-based batch normalization(SBN)というテクニックを使った。
掛ける数/割る数をそれより小さい整数のうちでもっとも2の冪小数に近い数で近似して、$\ll\gg$(both left and right binary shift)することで、掛け算の操作を回避しつつ、通常のBatch Normalizationと同様の性能を実現した。
重み$\mathbf{w}$とバッチ正規化のパラメータ$\theta$のUpdateについて
ADAMも重みのスケールの影響を減らしてくれるが、多くの掛け算の操作を必要とする。
Algorithm4で述べられているようなshift-based AdaMaxという方法を用いることで、掛け算の操作を減らしつつ、ADAMと同様の性能を実現した。

sign関数の微分が0になる問題
$$ q=sign(r) $$
において、$ \frac{\partial C}{\partial q} $ の推定値$g_q$が既知のとき、
$ \frac{\partial C}{\partial r} $ の推定値$g_r$を以下の式によって推定する。
$$ g_r = g_q1_{|r|\leq1}$$
このような推定では、$|r|$が小さいは、勾配情報がそのまま保存される。(straight-through estimator) 大きいときは勾配は0となるが、このようにしないと、モデルのパフォーマンスは悪化する。
$$1_{|r|\leq1}$$
は、
$$Htanh(x) = Clip(x, -1, 1) = max(-1, min(1, x))$$
の導関数でもある。つまり、上の推定は、勾配計算の都合上$sign(x)$を$Htanh(x)$とみなしていると解釈することができる。
予測時

1層目の処理
1層目の入力だけbinaryではないが、著者によると大きな問題ではない。
というのも、連続量をm bitの不動点として扱うことができ、
$$ s = x \cdot w^{b} $$
$$ s = \sum_{n=1}^{8} 2^{n-1} (x^n \cdot w^b) $$
により1層目の重みと入力の積が計算可能だからである。
XnorDotProduct
XNOR Table
| x | y | z |
|---|---|---|
| -1 | -1 | 1 |
| -1 | 1 | -1 |
| 1 | -1 | -1 |
| 1 | 1 | 1 |
$ x \times y = z $の関係にあることがわかる。
内積計算は掛け算して足すという操作に相当する。掛け算の部分をbit毎にXNORゲートで計算するような内積計算を本論文ではXNORDotProductと読んでいる。
結果
実験の条件を整理
| Torch7 | Theano | |
|---|---|---|
| Activations | Stochastically binarized | Determinasitically binarized |
| Batch Normalization | shift-based BN | vanilla BN |
| Learning rule | shift-based AdaMax | ADAM |
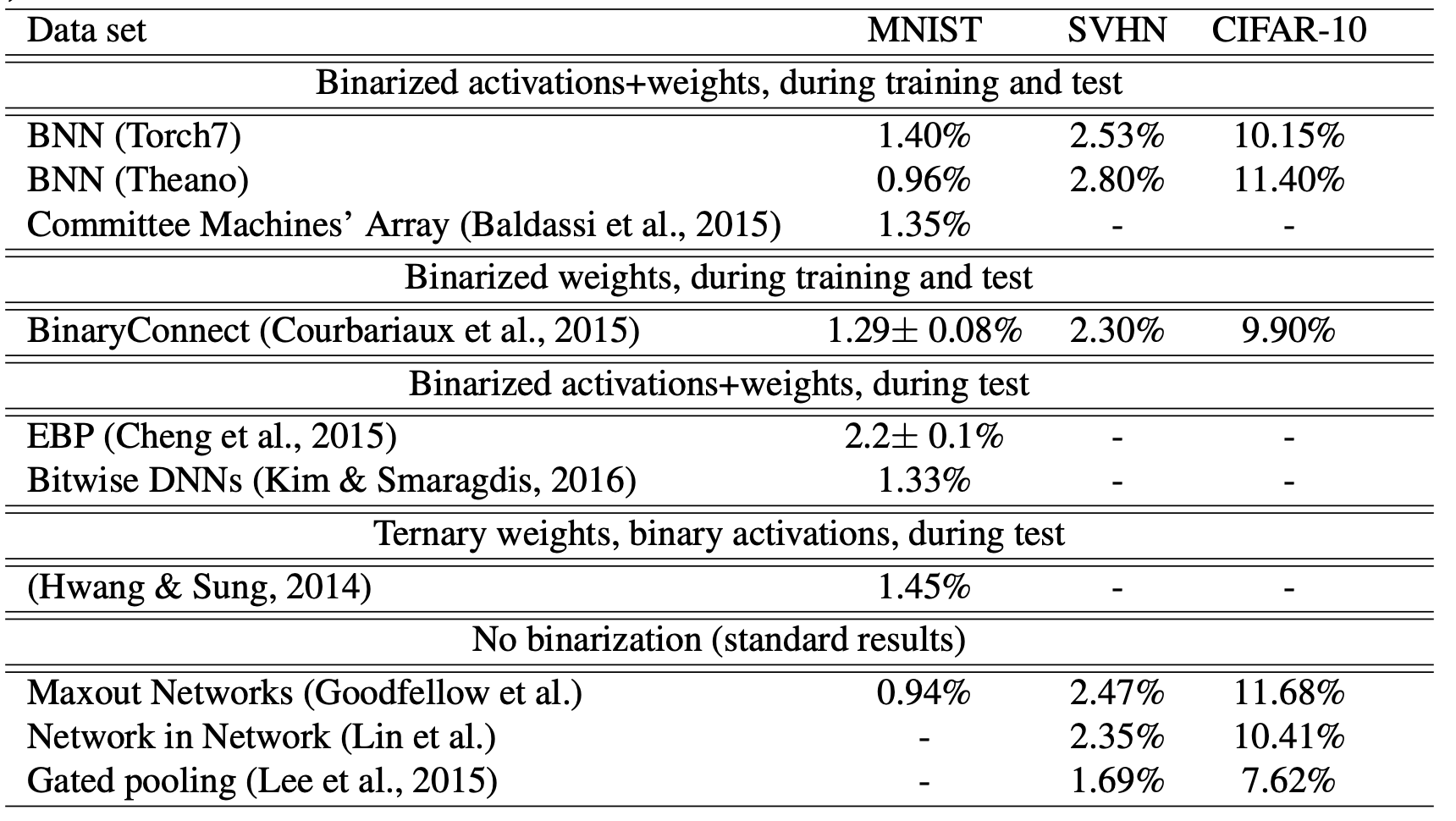
モデルの汎化性能
- Binary Connect よりも性能は落ちる。
- Committee Machines’ Array (Baldassi et al., 2015)は畳み込み層を持つモデル対応していない。
- 学習、推論が低電力で行えることと汎化性能のトレードオフがある。
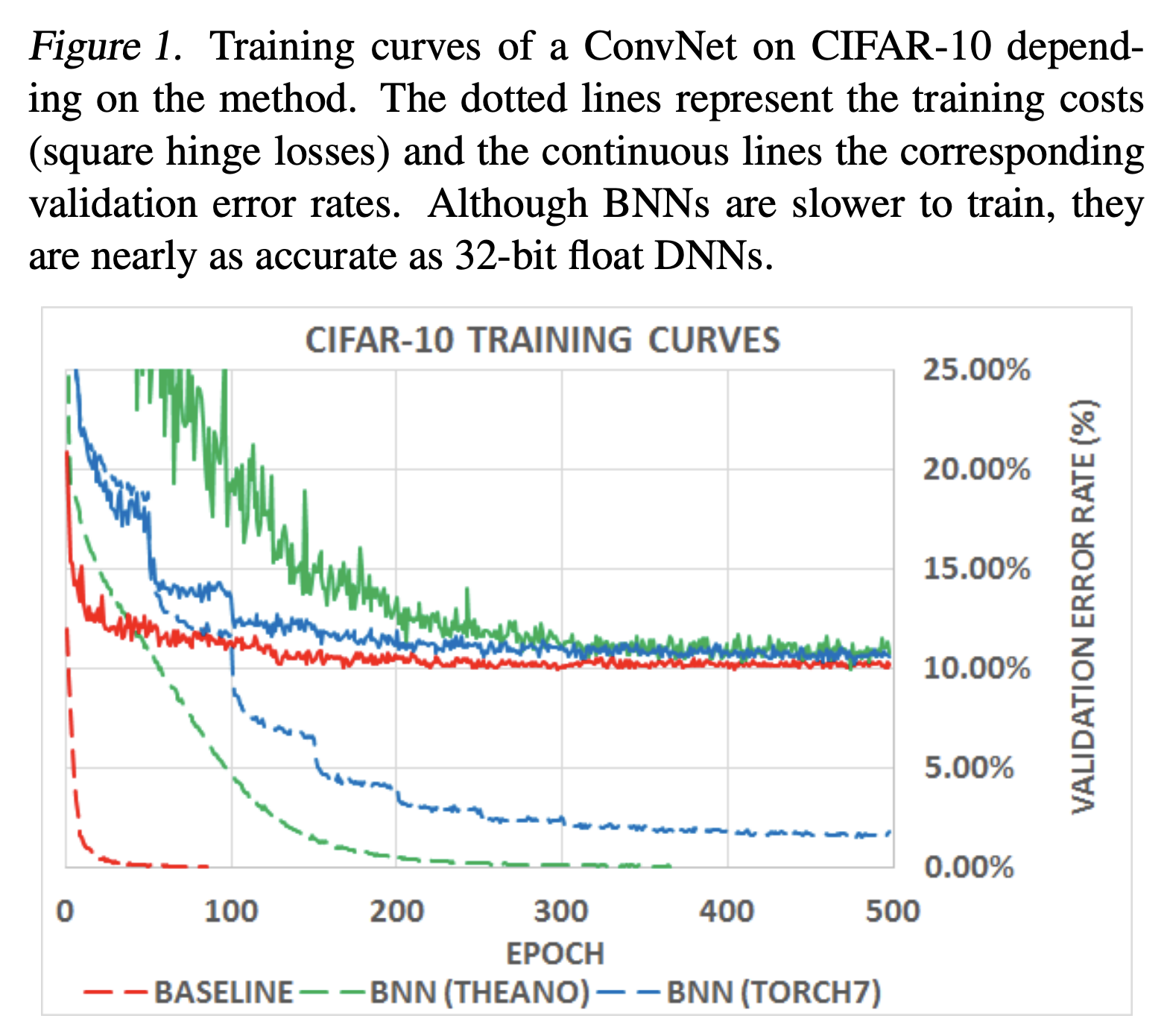
学習曲線
- 学習にかかる時間はBNNsの方が遅くなっている
- shift-basedのBNNの方がそうでないBNNsよりも学習が遅い。
- アーキテクチャの問題?
- 最終的には通常のDNNsに近い値に収束する。
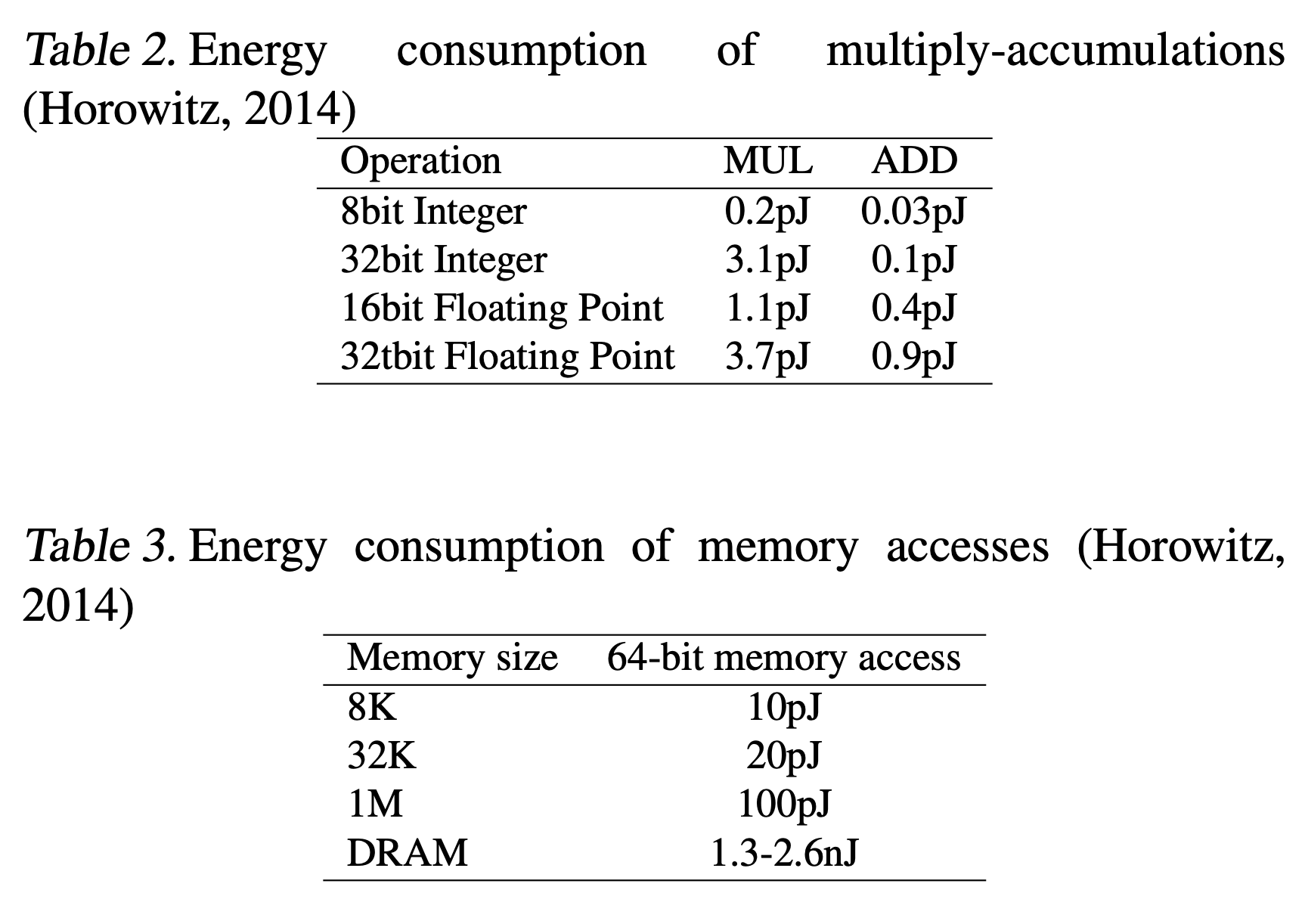
電力効率
- BNNsは特に、train時の順伝播計算と、推論時のエネルギー効率が大変良く、メモリサイズとアクセスを減らすことができる。
- 活性の2値化は、特に畳み込み層を持つモデルで計算を効率化できる。
- 重みの自由度よりもユニットの方がずっと多いため。
- 下の表から、積-和計算やメモリアクセスを減らすことの恩恵の大きさがわかる。
- 通常のDNNsでは32bitの実数の積を求め総和をとっていたが、それがBNNsでは1bitでできる。
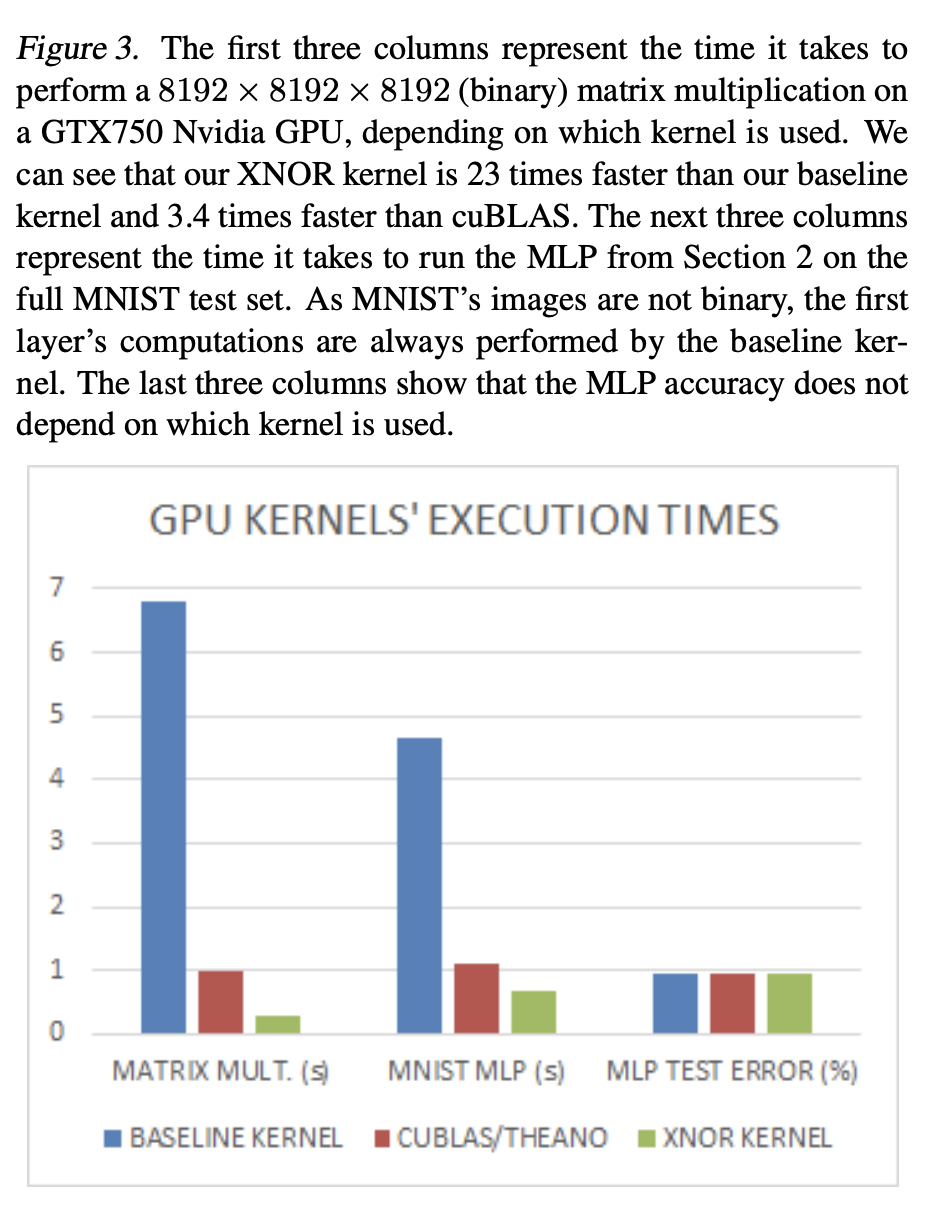
BNNsに最適化したGPUと通常のGPUの比較
- MLP(BNNs)によるMNISTの推論が、性能を保ったままふつうのKernelよりも7倍高速化できた。
結論と展望
- Trainの逆伝播、パラメータ更新のところで最適化の余地がある。
- 特に、パラメータ更新を実数で持たなければならない点がボトルネック。
- 他のbentchmarkの結果を増やす。