Binary Neural Network その３：「XNOR-Net」を読みました
インターンの中村です。
今回はXNOR-Netという論文を読んだので解説します。
またXNOR-Netの関連論文も解説していますので、よかったら見てください。
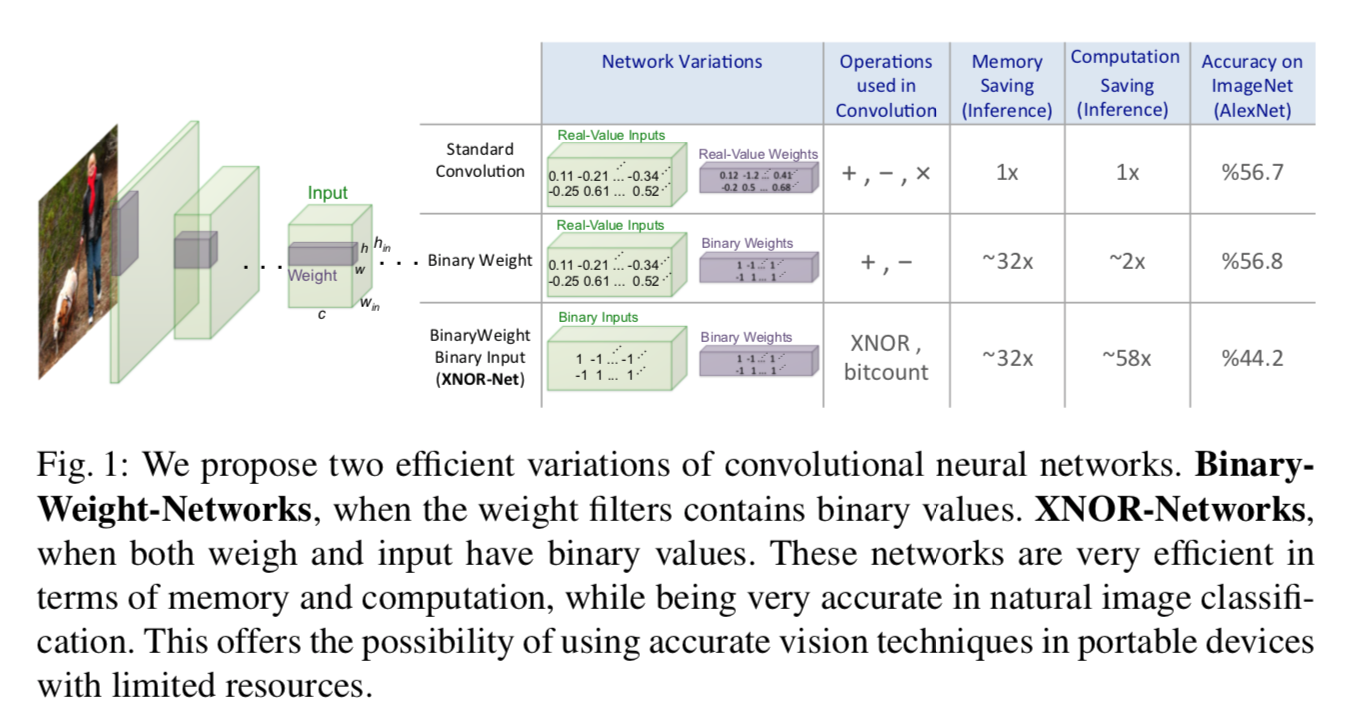
この論文ではBinary Neural Networkの 係数(scaling factor) を計算することにより、本来のニューラルネットワークに層の出力結果をより近づけ、性能を向上させることを提案しています。
新規性
- 重みがbinarizeされたBWN(Binary Weight Network)、及び、入力・重みの両方がbinarizeされたXNOR-Netを提案
- これらでは係数scaling factorを計算する
- 計算が早い
- 性能も良い
- ブロックの順番を入れ替えることにより性能が向上することなどの考察
1.重みがBinarizeされたBWN
画像$\mathbf{I}$が入力された時、フィルタ$\mathbf{W}$をバイナリフィルタ$\mathbf{B}$, スカラーである係数$\alpha$で近似します。
すなわち
$\mathbf{I} * \mathbf{W} \approx(\mathbf{I} \oplus \mathbf{B}) \alpha$
（ただし、$\oplus$は2値化された内積）
この時、目的関数は
であり、これを偏微分をつかって解くと
になります。それぞれ重みの符号、重みの絶対値の平均値となっており、直感的にも納得の行きやすい数字ですね。 これによって近似されたWを$\widetilde{W}$と呼びます。すなわち$\widetilde{W}=\alpha^{*} \mathbf{B}^{*}$です。 これを使ったNNを構築します。順伝播は$\mathbf{I} \oplus \widetilde{W}$とすれば良く、逆伝播はこれにchain ruleと積の微分公式を適用すれば
になるとわかります（ただし、2つめの式はこれ以前の論文で実験的に得られたテクニックに基づいているものであり非自明です）。これを使って計算していけばいいです。フィルタの計算が積ではなく足し引きで計算できるので、計算が早くなります。
これを発展させたXNOR-Netを考えます。
2. 重みも入力もBinarizeされたXNOR-Net
$\mathbf{I}$のうちコンボリューションされる範囲の入力$\mathbf{X}$、フィルタ$\mathbf{W}$が与えられた時（つまり$\mathbf{X}$と$\mathbf{W}$は同じ大きさです）、 $\mathbf{X}^{\top} \mathbf{W} \approx \beta \mathbf{H}^{\top} \alpha \mathbf{B}$ で近似します。すなわち、
$$ \alpha^{*}, \mathbf{B}^{*}, \beta^{*}, \mathbf{H} *=\underset{\alpha, \mathbf{B}, \beta, \mathbf{H}}{\operatorname{argmin}}|\mathbf{X} \odot \mathbf{W}-\beta \alpha \mathbf{H} \odot \mathbf{B}| $$
のような最適化問題と考えることができます。$\alpha$はコンボリューションフィルタ$\mathbf{W}$に対して単一の値ですが、$\beta$はウィンドウごと（コンボリューションする場所ごと）に異なる値だということに注意してください。 この問題は
$$ \mathbf{Y}_{i}=\mathbf{X}_{i} \mathbf{W}_{i},\mathbf{C} \in{+1,-1}^{n} \ \ \text{s.t. }\ \mathbf{C}_{i}=\mathbf{H}_{i} \mathbf{B}_{i} $$
および
$$ \gamma \in \mathbb{R}^{+} \ \text {s.t.}\ \gamma=\beta \alpha $$
とおくと
$$ \gamma^{*}, \mathbf{C}^{*}=\underset{\gamma, \mathbf{C}}{\operatorname{argmin}}|\mathbf{Y}-\gamma \mathbf{C}| $$
と書くことができ、BWNと同じ最適化問題と考えられるので
$$ \mathbf{C}^{*}=\operatorname{sign}(\mathbf{Y})=\operatorname{sign}(\mathbf{X}) \odot \operatorname{sign}(\mathbf{W})=\mathbf{H}^{*} \odot \mathbf{B}^{*} $$
を得、また自然な近似により
$$
\left(\frac{1}{n}|\mathbf{X}|_{\ell 1}\right)\left(\frac{1}{n}|\mathbf{W}|_{\ell 1}\right)\approx\beta^{*} \alpha^{*}
$$
を得ます。あとは$\alpha ,\beta$をこれに従って計算すればいいですね。
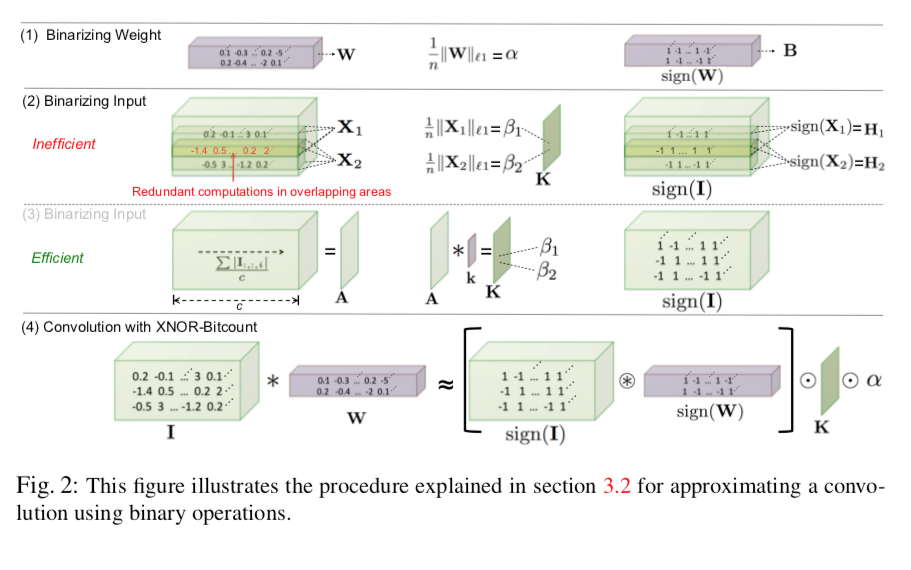
普通に考えると図2(1),(2)のように
- 重みをBinarize
- それに対して最適な$\alpha$を求める
- 入力をbinarize
- 最適な$\beta$をウィンドウそれぞれについて求める
という作業が入りますが、図2(2)ではなく図2(3)のようにすると$\beta$を効率的に求めることができ計算量を減らすことができます。
- Convolution windowごとに$\beta$を求めなければならないので、先にチャンネル平均をメモしておくことで高速化します。競プロ的なテクニックですね。
数式で書くと次のようになります：
$\mathbf{A}=\frac{\sum_i\left|\mathbf{I}_{:, :, i}\right|}{c}$（チャンネル平均を取る）
$\mathbf{K}=\mathbf{A} * \mathbf{k}\ \mathrm {\ where\ } \forall\ i,j\quad\mathbf{k}_{i j}=\frac{1}{w \times h}$
この結果、$\mathbf{K}$は求めたい$\beta$の行列になっている、よって
として近似を得る（ただし、$\otimes$はXNOR積）
パフォーマンス比較
XNOR-Netは文字通り重みと入力のXNOR（一致するなら$1$、一致しないなら$-1$）を取るだけなので、コンボリューション部の計算が非常に速いです。理論上、CPUはきちんと実装すれば1クロックで64bitのXNOR計算ができるので $S=\frac{c N_{\mathbf{W}} N_{\mathbf{I}}}{\frac{1}{64} c N_{\mathbf{W}} N_{\mathbf{I}}+N_{\mathbf{I}}}=\frac{64 c N_{\mathbf{W}}}{c N_{\mathbf{W}}+64}$
- ただし、$c$:チャンネル数,$N_{\mathbf{W}}$:ウィンドウの大きさ、$N_{\mathbf{I}}$:入力画像の大きさ
倍になります。これは、例えばResNetの多くのコンボリューションにおけるパラメータ($c=256,N_{\mathbf{I}}=14^{2}, N_{\mathbf{W}}=3^{2}$)で62.27倍です。著者らはオーバーヘッドにより実際は58倍程度の性能を得たようです。
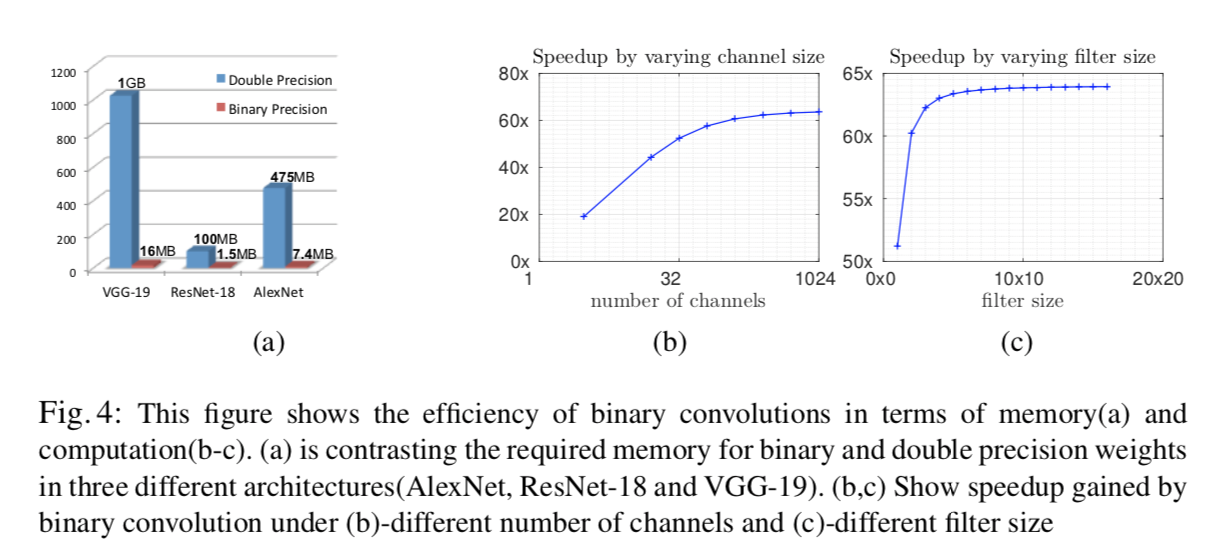
メモリサイズも非常に小さくなります。図4にわかりやすくまとまっているので参照してください。
性能比較
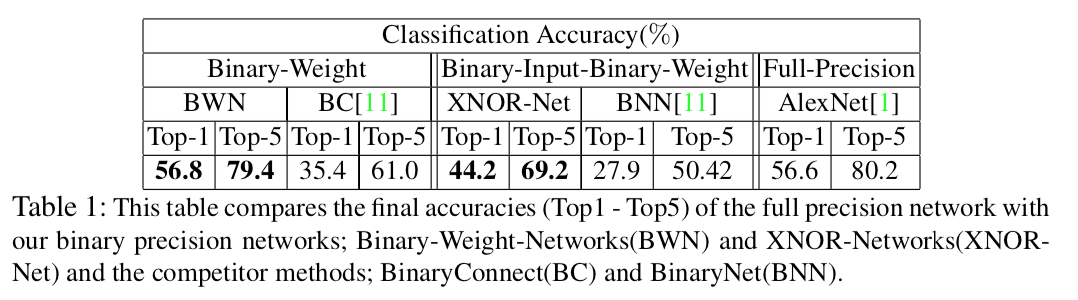
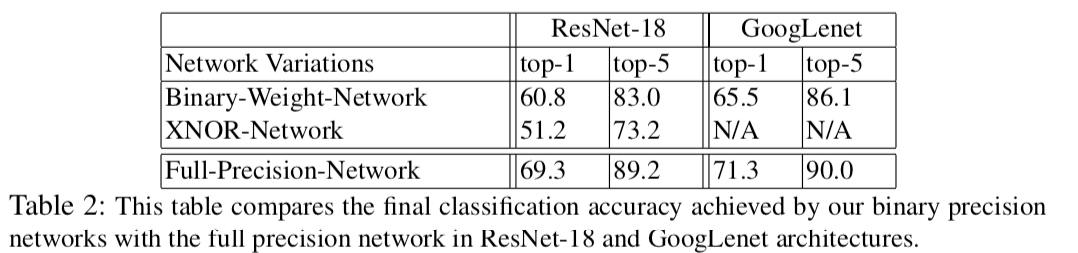
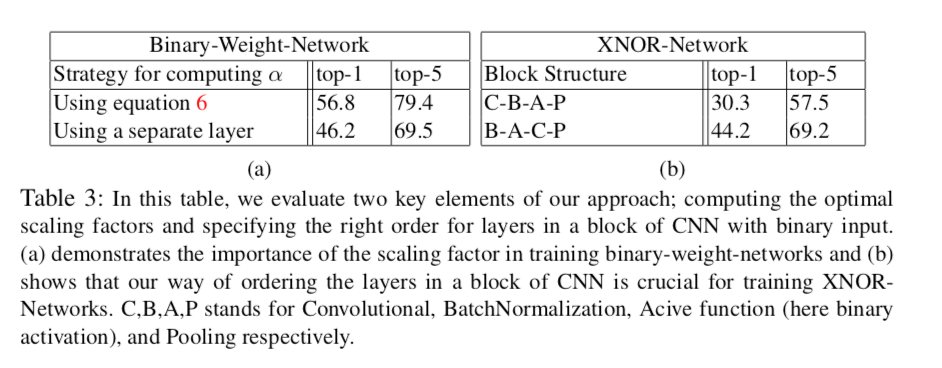
表1,2に示すように、提案手法であるBWN,XNOR-NetはこれまでのBinarize手法に比べ高い性能を示しています。
$\alpha$をバイアス項なしのAffine Layerと捉え(いわゆる$y=Ax+b$で$A$をスカラー、$b$をゼロと考えるわけですね)、独立した層として訓練することも可能ですが、結果としてはこれをやっても表3(a)に示されるように性能が下がってしまいます。これはパラメータ$\alpha$を$|\mathbf{W}|$の平均として計算するという方法が最適であることを示唆しているでしょう。
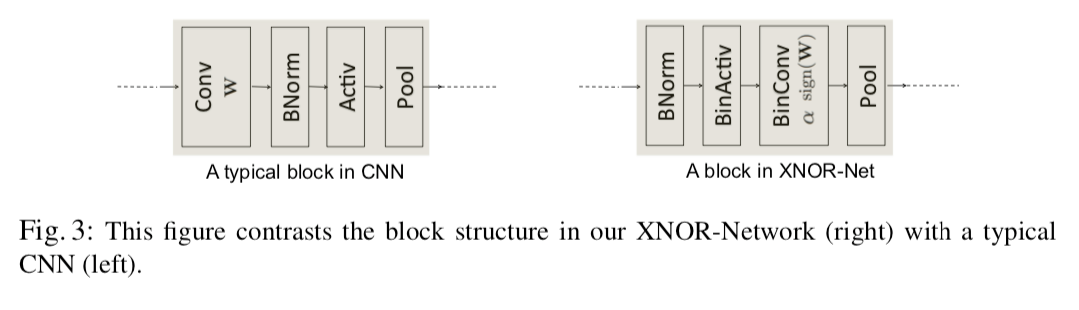また、表3(b)では図3のように層（ブロック）を入れ替えると性能が向上するということも示されています。この順番のほうが性能が良くなる理由として、
- Binarizeした直後にMax-Poolingをするとほとんどの要素が1となり情報が大量に失われてしまう
- BatchNormをすると平均が0になるので、その直後に0-thresholdであるBinarizeをするとそれによる誤差が少なくなる
事が考察されています。
今後の展望
実際にやってはいないようですが、以上の手法はk-bitの量子化に対しても容易に拡張できるとされています。$[\cdot]$を床関数として、入力$x\in[-1,1]$に対し
$$ q_{k}(x)=2\left(\frac{\left[\left(2^{k}-1\right)\left(\frac{x+1}{2}\right)\right]}{2^{k}-1}-\frac{1}{2}\right) $$ とするわけですね。
まとめ
この論文ではscaling factorと呼ばれる係数を2値化ニューラルネットに導入し、それらに対する理論的な考察によってその効率的な計算方法を与えることにより、良い時間・空間計算量、end-to-endで訓練することができるという性質を保ちつつ性能を大きく向上させました。 理論的考察のところはかなりバッサリ省略しながら書いたので、細かいところが気になった人はぜひ論文にあたってみてください。
なお、本記事はMETRICAの勉強会向けに作った資料を修正したものです。
