インターンの中村です。
今回はStyleGANを読んだので解説していきます。

NVIDIAの論文です。GPU開発元らしく潤沢なGPU資源を使って超リアルな画像を生成した¹ことで話題になりましたが、特徴をレベルごとに分離するGeneratorの構造が独特で内容的にも面白いです。

この記事では、GANの基礎をさらっとさらい、そのあとでStyleGANのアーキテクチャの説明をします。

GANって何

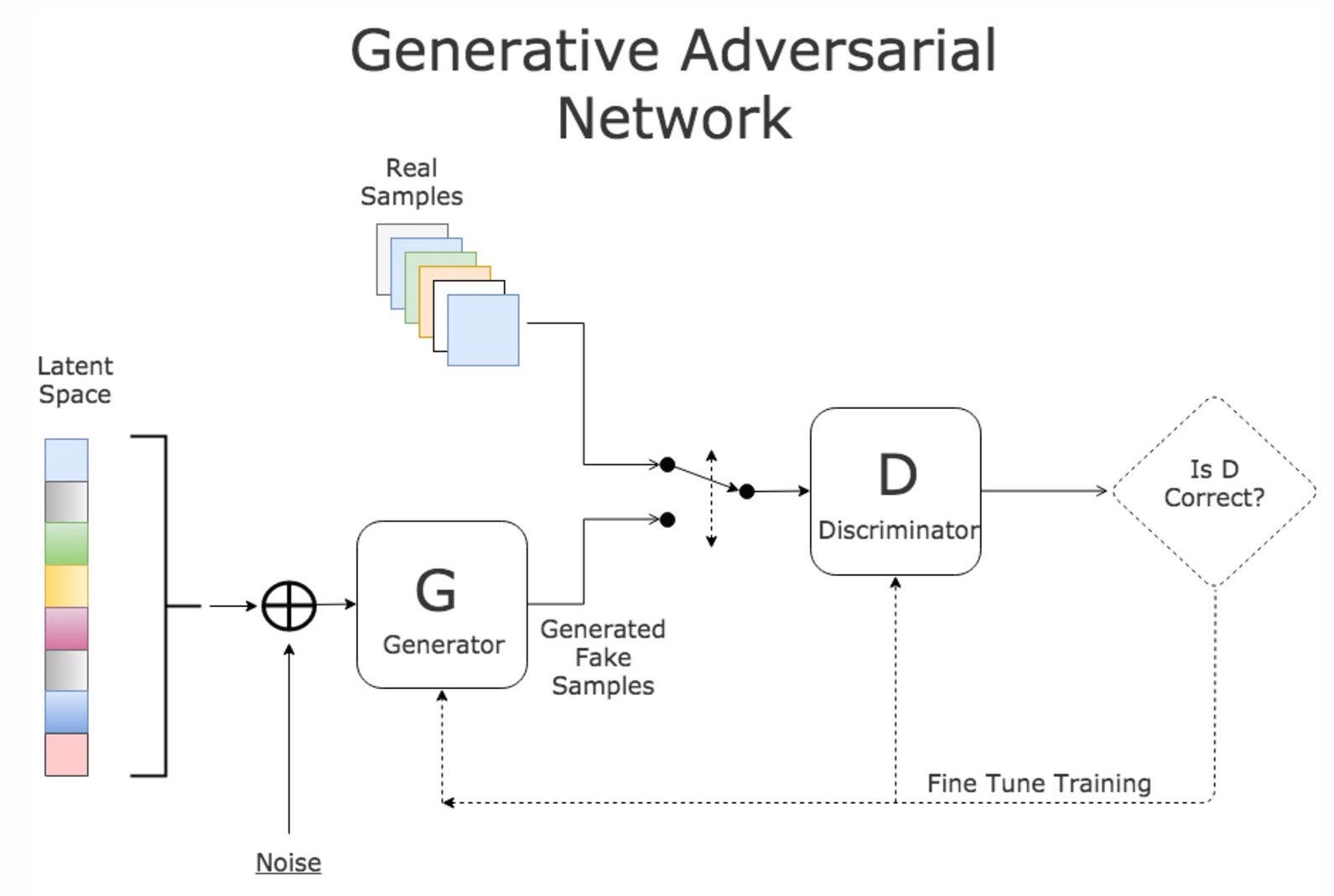
生成モデル(Generator)を敵対モデル（Adversarial Net,「真贋を判定するもの」なのでDiscriminatorとも)と同時に訓練させることで生成されるもの（画像、音声etc...）の質をあげようという試み

$$ \mathcal{L}_{G A N}(G, D)= \mathbb{E}_{y} [ \log D(y) ]+ \mathbb{E}_{z} [\log (1-D(G(z)) ] $$

$G$はこれを小さくしようとし（=$D$を騙そうとし）、敵である$D$は大きくしようとする（見分けようとする）。 損失関数が定義されているので、深層学習モデルを$G$や$D$に使うことも可能（最近は全部そう）。

例題

https://qiita.com/taizan/items/cf77fd37ec3a0bef5d9d

これの$G,D,z,y$は何？

答え

$G$: 線画から色付き画像を生成するもの
$D$: 色付き画像が「イラストレーターに作られたもの」か「$G$に塗られたもの」か判定するもの
$z$: 線画。したがって、$G(z)$が偽物の色付き画像になる
$y$: イラストレータに作られた、本物の色付き画像

本論文

Generatorの新たなアーキテクチャを提案
最初の層ではなく途中の層に確率的な影響を追加する
- スタイル$A$を追加
- 確率的な影響$B$を追加
これにより「スタイル（人物の同一性などの大きい特徴）」「確率的な影響（そばかすや髪の位置）」「その大きさ」をネットワークの構造において分離した

緑の箱が学習可能な要素。

定数の入力からスタートし、"スタイル”を途中の層にAdainで追加する（左側のA）
- フィルタの出力を正規化したあと、チャンネルごとに異なる１次関数を掛けている
- つまり、いわゆる切片と傾きが箱A（に入ってくる乱数$\mathbf{w}$）で決定される。下の式では$\mathbf{y}$と書かれている

$$ \operatorname{AdaIN} \left( \mathbf{x}_{i} , \mathbf{y} \right) = \mathbf{y}_{s, i} \frac{\mathbf{x}_{i} - \mu \left( \mathbf{x}_{i} \right) }{\sum \left( \mathbf{x}_{i} \right)} + \mathbf{y}_{b, i} $$

さらに定数倍したノイズを追加（右側のB）
この研究では損失、正則化、ハイパラの新規性はなし。Gの構造のみが提案されている

結果

それぞれの変更としては、

C: Adain演算を追加
D: 最初の層の入力を定数に

これまでのGでは乱数が一般的だったので、これにより性能が上がったのには驚きである

E: ノイズ入力（Bを$\oplus$してるやつ）を追加
F: 時々、異なる層には別の$\mathbf{z}$から生成された$\mathbf{w}$を入力してやった（スタイルミキシングと呼んでいる）

別の層に入力されたスタイルに関連性はないんだ、と教えてやる意味を持つ
ただ、この表の評価からするに効果はあったりなかったり

定性的評価

AdaIN演算

最初の方の層(Coarse: 4x4/8x8)の$A$を取り替えると姿勢、髪型、顔の形、眼鏡といった高レベルな特徴が取り替えられる真ん中の層だと表情、目の開閉、細かい髪型といった特徴が、最後の方の層(Fine: 64x64-1024x1024)だと色の雰囲気や微小な要素のみが変わる

モデルFは特に複数のノイズから生成されたLatent Codeを混ぜながら（スタイルミキシングしながら）スコアを取ると点数が良い（→自然な画像が生成されている）

Noise加算

ノイズによって髪が細かく変わっているのがわかるこのように、そばかすや髪の流れといった確率的に決まる要素がノイズ加算によって決定されるようだ (c)はノイズによって変化しやすい場所を表した図。頬と髪などをくらべるとわかりやすい

(a)ノイズあり
(b)ノイズなし
- 「画家っぽい」感じに
(c)Fine Layersのみにノイズ
(d)coarse layersのみにノイズ

ノイズを加える場所によって生成される背景や巻き髪のスケールが違うのがわかる

Latent Codeのdisentanglement

そもそも、データセットが何らかの領域を欠いている可能性あり(a)
- 例えば、「長い髪の女」「短い髪の女」「短い髪の男」はいるけど「長い髪の男」はいないみたいな
それを、きれいな形をした$\mathcal{Z}$から生成するように訓練すると空間が曲がる(b)
- $\mathcal{Z}$を無理に訓練データに対応させた結果
- これをlatent codeのentanglementと呼んでいる
しかし、今回のモデルではFCNによって$\mathcal{W}$に写像してからCNNに入れている
(c)のほうがリアルな画像を生成しやすいし、俺たちのStyleGANのFCNもこのような$\mathcal{W}$への写像を獲得してんじゃね？（予想）

定量評価

というわけで実際に評価してみた

Path LengthとSeparabilityの２つがある：これらもこの論文で提案された手法である

Path Length

適当に選んだ２つの乱数 $\mathbf{z}_1, \mathbf{z}_2$ を $t\in[ 0,1 ]$ で内分した点を考える。更にそこから微小にずらした点（$t+\epsilon$で内分した点）も考える
それらを種にして生成された画像をVGG16モデルにかけ、その中間活性の距離を取る（それが下の式の$d$）
その平均を取る

$$ l_{\mathcal{Z}}=\mathbb{E}[\frac{1}{\epsilon^{2}} d\left(G\left(\operatorname{slerp}\left(\mathbf{z}_{1}, \mathbf{z}_{2} ; t\right)\right),G\left(\operatorname{slerp}\left(\mathbf{z}_{1}, \mathbf{z}_{2} ; t+\epsilon\right)\right) \right) ] $$

つまりこう↑
StyleGANだと$\mathcal{W}$にマップされているので

$$ l_{\mathcal{W}}=\mathbb{E}[\frac{1}{\epsilon^{2}} d\left(g\left(\operatorname{lerp}\left(f\left(\mathbf{z}_{1}\right), f\left(\mathbf{z}_{2}\right) ; t\right)\right),g\left(\operatorname{lerp}\left(f\left(\mathbf{z}_{1}\right), f\left(\mathbf{z}_{2}\right) ; t+\epsilon\right)\right) \right) ] $$

こう↑なる
結果、StyleGANのほうが小さかった
$t \in\{0,1\}$にする（選んだ２つの点の付近だけで計算する）とさらに小さくなった
- 表中ではendと書かれているところ
- $\mathcal{Z}$に実際には逆像の存在しない$\mathcal{W}$の領域（上の例でいう長い髪の男）について距離を計算することがなくなったためか

この指標にはどのような意味合いがあるのか？

当然ある程度の距離は（異なる画像の中間活性なのだから）生まれるものと考えられるが、変化が不自然/激しいと大きくなる
- 例えば、生成画像が大人の男から女に変化する途中で一旦子供になったり、ましてや人間でないものに変化していたりしたら大きくなってしまうだろう
- つまり、これが小さいことは変化が（VGG16にとって≒人間の視覚にとって）「線形」に近いということになる。なので小さい方がentanglementを解消できていることになり嬉しい

Separability

たくさん(20万サンプルとか）生成する
別の分類器で特定の特徴について分類する
- ex.男か女か
確信を持って分類されているもの上位10万個を選ぶ
これらのサンプルを生成したLatent Code$\mathbf{w}$がどのくらい多次元超平面でSeparableなのかを線形SVMで分離して予測する
エントロピー$\mathrm{H}(Y | X)$を算出
- $X$がSVMの予測
- $Y$が分類機の予測
- 「超平面のどちらに$\mathbf{w}$がいるのかがわかったとき、実際の予測クラスを知るのに必要な追加情報量」に相当する。なので低いほうが良い
40種類の特徴について$\exp \left(\sum_{i=0}^{40} \mathrm{H}\left(Y_{i} | X_{i}\right)\right)$を計算する
StyleGANのほうが強かった
FCNの深さを上げると、画像の質、Separabilityともに良くなった
- 既存モデルに同じようにFCNを導入すると、$\mathcal{Z}$におけるSeparabilityは大きく低下するものの(10.78→170.29)、$\mathcal{W}$においてはやっぱり下がっている
- 今回のモデル・既存のモデル両方でFCNがentangleを解消する役に立ってる！

感想

スタイル変換の文脈でよく使われていたAdaINをGANに持ち込んだことにより、特徴をレベルごとに独立に生成できるようになったこと、ノイズをFCNによってマップしたうえで$G$に導入することでデータ不均衡によるノイズ空間の歪みを是正する仕組みとしたことが大きなcontributionと言えるでしょう。脚注にも示したWaifuLabsはStyleGANのこの特性を大いに利用して、インタラクティブにスタイルを選びながら画像を生成できる良質なデモになっているので是非試してみてください。

この記事はMETRICAの内部勉強会用の資料を改稿して作りました