OpenPoseで実装されているHand推定の論文「Hand Keypoint Detection in Single Images using Multiview Bootstrapping」を読みました

CTOの幅野です。
OpenPoseのHand Keypoint検出モデルの論文を読みましたの解説していきます。

概要

RGB画像から手の部位を検出するモデルの学習方法を提案。
Pose推定などで利用されているConvolution Pose Machinesを手の部位検出に応用することを考える。
Depthを利用した検出方法と同等の精度を達成した。

Convolutional Pose Machine(CPM)

Convolutionで構成される、RGB画像からPoseの各部位のヒートマップを出力するネットワーク

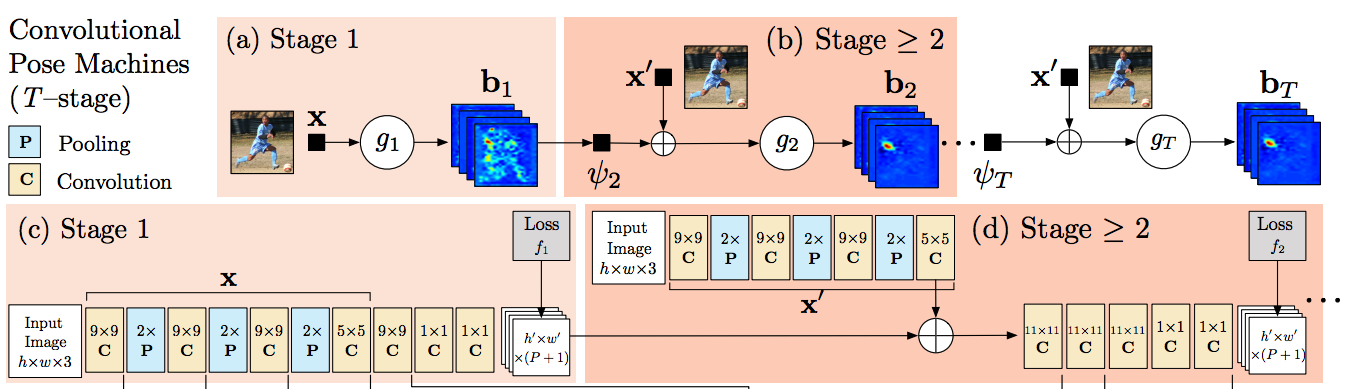
Stageごとにヒートマップが出力され、それぞれに対してヒートマップの損失関数を計算し学習を行う。多段にするは他の部位ヒートマップ情報を利用すること。本論文では手の検出にこのモデルを応用する。

手の部位検出までの流れ

RGB画像から手の部位を検出するまでに２段階の工程を利用している。

手のBounding Boxの検出、Crop
Cropした画像を元に手の部位を検出

2はCPMを利用して部位を検出するが、そのために手の部分を1で抽出している。手の部分を抽出するためにOpenPoseによって推定した手首と肘を利用する。手の中心座標は肘から手首への延長線上にあると仮定する。具体的な計算方法は肘から手首の長さの0.15倍を延長した点を手の中心座標としている。 Bounding Boxの大きさは学習時には全ての手の部位が包含できる最大サイズ$B$を2.2倍したものとし、テストの推論時には$B$をOpenPoseで推定したHeadからBottomまでの長さの0.7倍として計算する。

Cropした画像は以下のようになる。

学習の問題点

手の部位を検出する際に出てくる問題は教師をつけることが難しいという点である。その理由は以下の画像のようにオクルージョンが発生するためである。

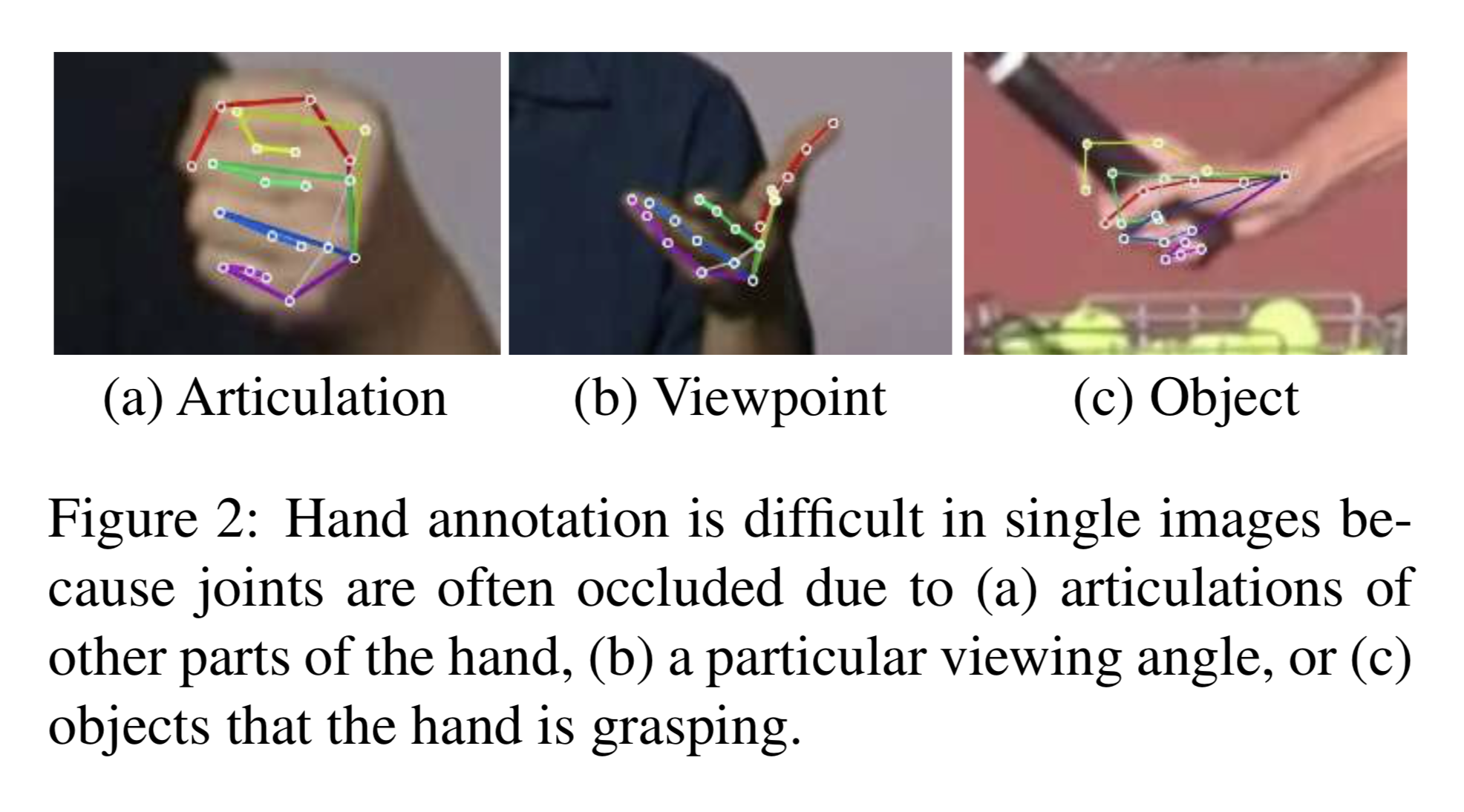
手の部位はPoseと比較すると「握る」などの動作があるためオクルージョンを起こす確率が高い。そしてこのオクルージョンしている画像に対してほぼ確実に教師をつけることは困難である。

BootStrappingを利用した学習

本論文では上の問題に対してMulti Cameraの情報を利用することで教師のない画像に教師をつけて再学習するBootStrapping手法を提案している。

なお、この手法を利用するための前提として教師がつけられていない画像には以下の条件が設定されている。

キャリブレーションされた複数カメラによって同フレームで撮影された画像が用意されていること

大まかな手順は以下の通りである。

教師のついている画像を利用してCPMのモデル$d_0$を学習
$d_0$を使って教師のついてない画像を推論, 3次元情報の抽出
Confidense Scoreの高い順に画像をソートし、上位N個を学習データに加えて再学習

3次元情報の再構成を利用して教師を作成

この手法は同じフレームで撮影された複数画像を元に３次元の部位座標を再構成することで、教師を新たに付与している。

学習した$d_0$を利用して教師のついていない画像$I_v^f$に対して部位の検出を行う。

$$ \mathcal{D} \leftarrow\left\{d_{i}\left(\mathbf{I}_{v}^{f}\right) \text { for } v \in[1 \ldots V]\right\} (5) $$

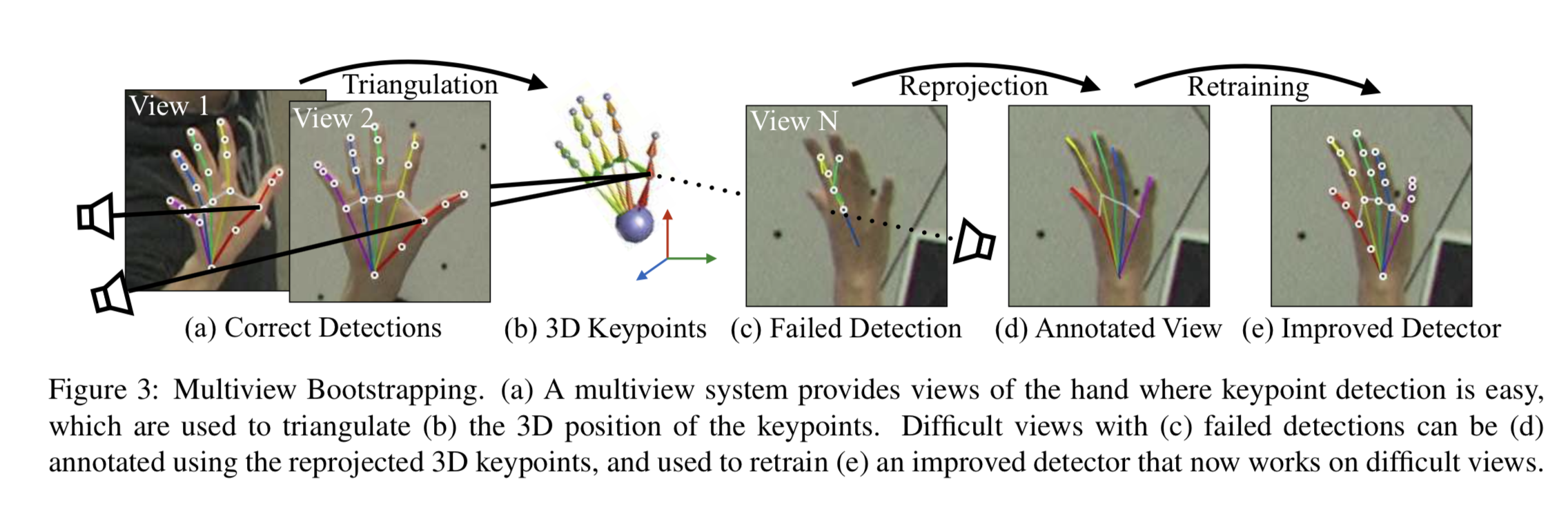
これらを元に3次元情報を構築するのだが、外れ値をなるべく減らすようにConfidence Scoreが$\lambda$以下の関節点は除去する。検証時は$\lambda=0.2$としている。

上図のように2つの2次元情報$\mathbf{x}_{p}$とカメラのキャリブレーションを元に3次元情報$\mathbf{X}_{p}^{f}$を構成することができる。

同フレームに$V$個の画像があった場合、${}_V C_2$個の3次元情報の候補が作成できる。

この中から以下の式が最小になる3次元情報を採用する。 $$ \mathbf{X}_{p}^{f}=\arg \min_{\mathbf{X}} \sum_{v \in \mathcal{I}_{p}^{f}}\left|\mathcal{P}_{v}(\mathbf{X})-\mathbf{x}_{p}^{v}\right|_{2}^{2} (6) $$

追加する学習データの選択

本手法では新たに教師を付けたデータを学習データとして追加するときにランダムに追加するのではなく$d_0$で推定されたConfidence Scoreの高いフレームを追加する。スコアリングの計算は以下の通りで各フレームごとに計算する。

$$ \operatorname{score}\left( \left\{ \mathbf{X}_{p}^{f} \right\} \right)=\sum_{p \in[1 \ldots P]} \sum_{v \in \mathcal{I}_{p}^{f}} c_{p}^{v} (7) $$

$score$を利用して上位$N$個を学習データとして追加したものを$\mathcal{T}_{i+1}$とし、再学習を行う。 f:id:metrica-tech:20190907140838p:plain

結果

本手法の検証を行うためにMPII、NZSLという手が写っているデータセットに教師をつけた。 MPIIは1300、NZSLは1500の手の学習データを作成し、2000枚を学習用、800枚をテスト用に利用した。

学習は"Render", "Manual", "Mix"という3種類の方法を利用して検証を行っている。

Render: UnrealEngineを利用して11000枚の合成画像を元に学習
Manual: MPII, NZSLの学習データを利用して学習
Mix: RenderとManualを組み合わせて学習

なお、これらの学習データに加えて、教師のないPanoptic Studio DatasetでMultiview Bootstrappingを行っている。

Panoptic Studio Datasetは31個のHDカメラで撮影されたデータセットである。

一つの指標として$PCK$という手法を利用して検証を行っている。 f:id:metrica-tech:20190907141819p:plain

PCKによる検証

MPI, NZSLのテストデータに対してのPCKの評価が以下の図である。

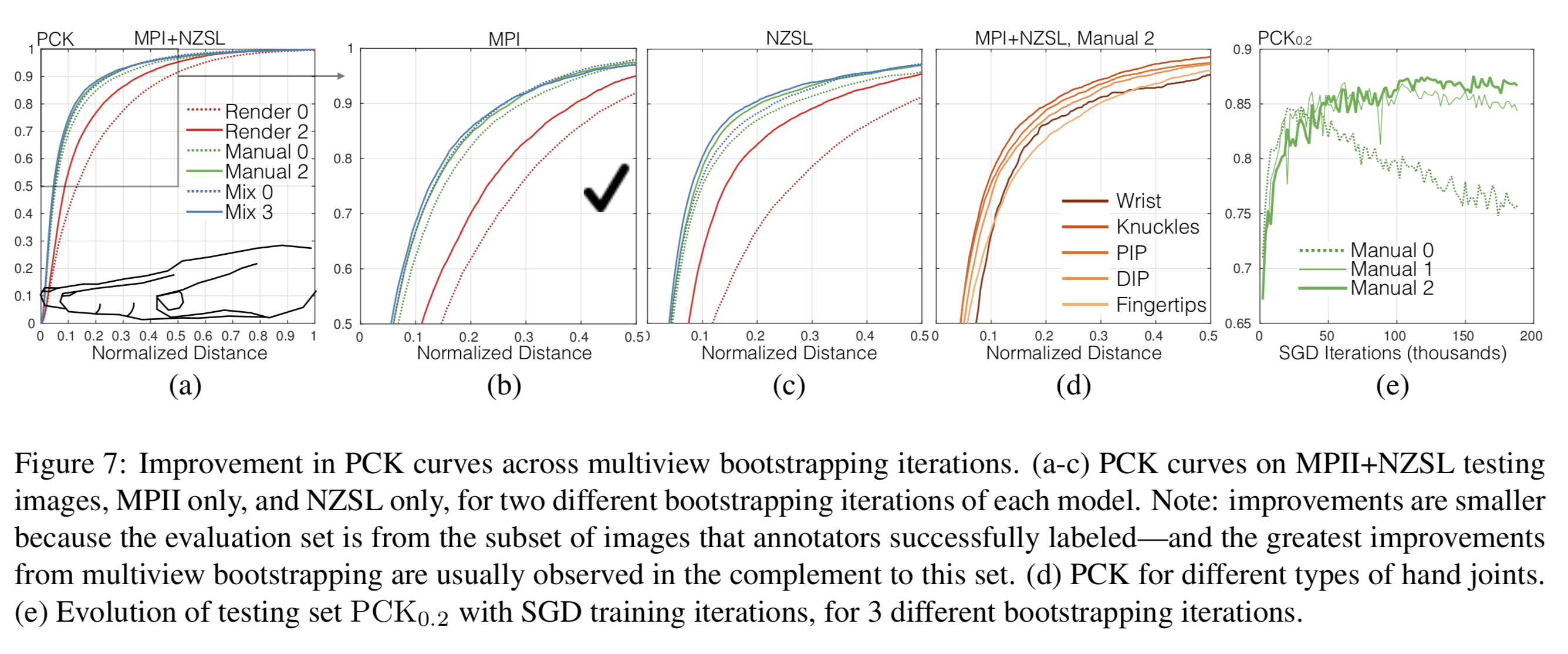
縦軸がPCK, 横軸が[0, 1]で正規化された距離の閾値 $\sigma$ である。 $\sigma$ の値が低いときにPCKが高いほど精度が良い。

(a)のモデルで記載されてある番号（"Render 0"）などはMultiview Bootstrappingによって再学習した回数である。 (a)を見ると、Bootstrappingをすることによって精度が向上しており、Mixが一番高い性能を出している。 (e)は縦軸が $\sigma = 0.2$ のときのPCK、横軸がSGDのiterationを表している。これを見ると再学習を加えることによって、iterationを増やしても過学習がおきにくいロバストなモデルを構築できていることがわかる。